Propósito de la sesión:
Expresamos con lenguaje algebraico el conjunto solución de una condición de desigualdad, Asimismo, justificamos las propiedades de las desigualdades usando ejemplos y con nuestros conocimientos matemáticos, y corregimos errores si los hubiera.
Saberes previos:
Leemos y respondemos:
Repasamos:
INTERVALOS
Son subconjuntos de números reales y se utilizan para expresar gráficamente la solución de las inecuaciones, estos se representan en la recta numérica real. Pueden ser abiertos o cerrados, finitos o infinitos.
Siendo los intervalos subconjuntos de los números reales, es posible realizar con ellos las propiedades operativas de los conjuntos, como son la unión y la intersección.
CLASIFICACIÓN DE INTERVALOS:
INECUACIONES DE PRIMER GRADO
A. CONCEPTO:
ax + b > 0
ax + b < 0
ax + b ≤ 0
ax + b ≥ 0
C. SOLUCIÓN DE UNA ECUACIÓN:
Para resolver una inecuación se utilizan las propiedades de las desigualdades y de los números reales que nos lleva a una desigualdad equivalente.
Esto significa que la nueva desigualdad tiene el mismo conjunto de soluciones que la dada.
Todos los números que satisfacen la desigualdad constituyen el conjunto solución.
D. PROPIEDADES:
- Propiedad Aditiva
- Propiedad Multiplicativa
E. EJERCICOS DE APLICACIÓN:
VÍDEO 2
VÍDEO 3
VÍDEO 4
VÍDEO 5
Problemas con inecuaciones:
Actividad:













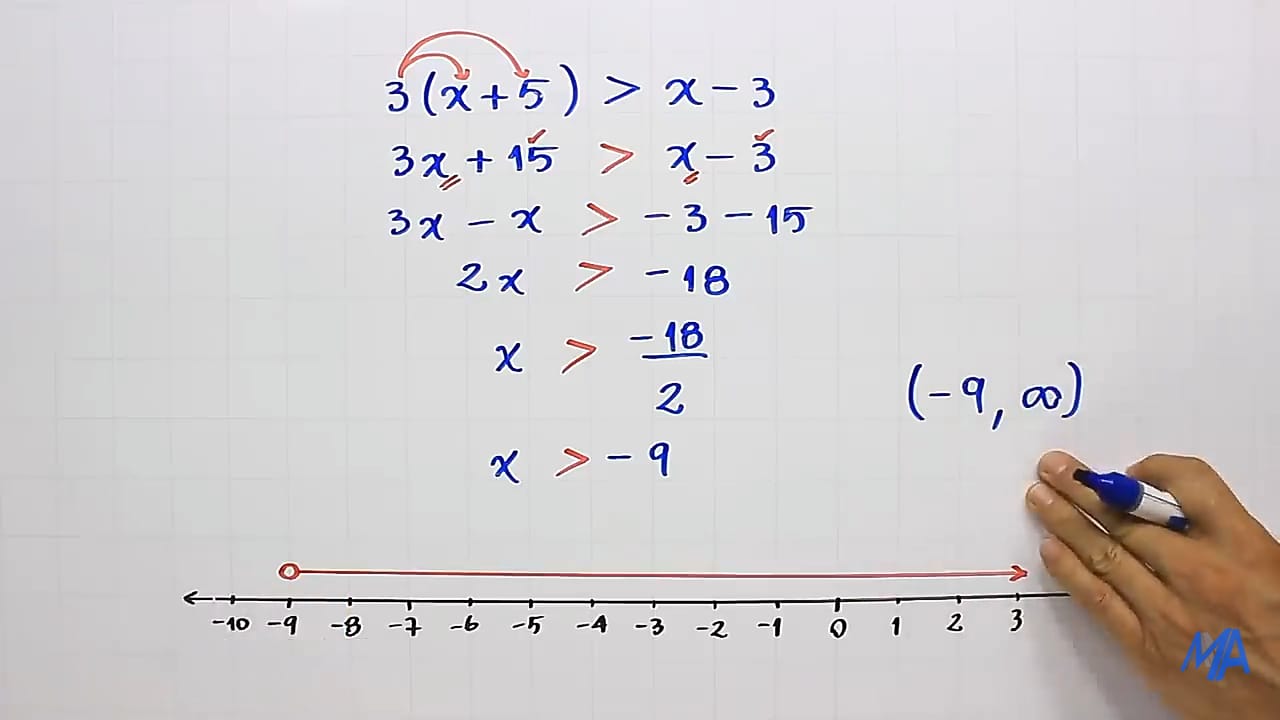
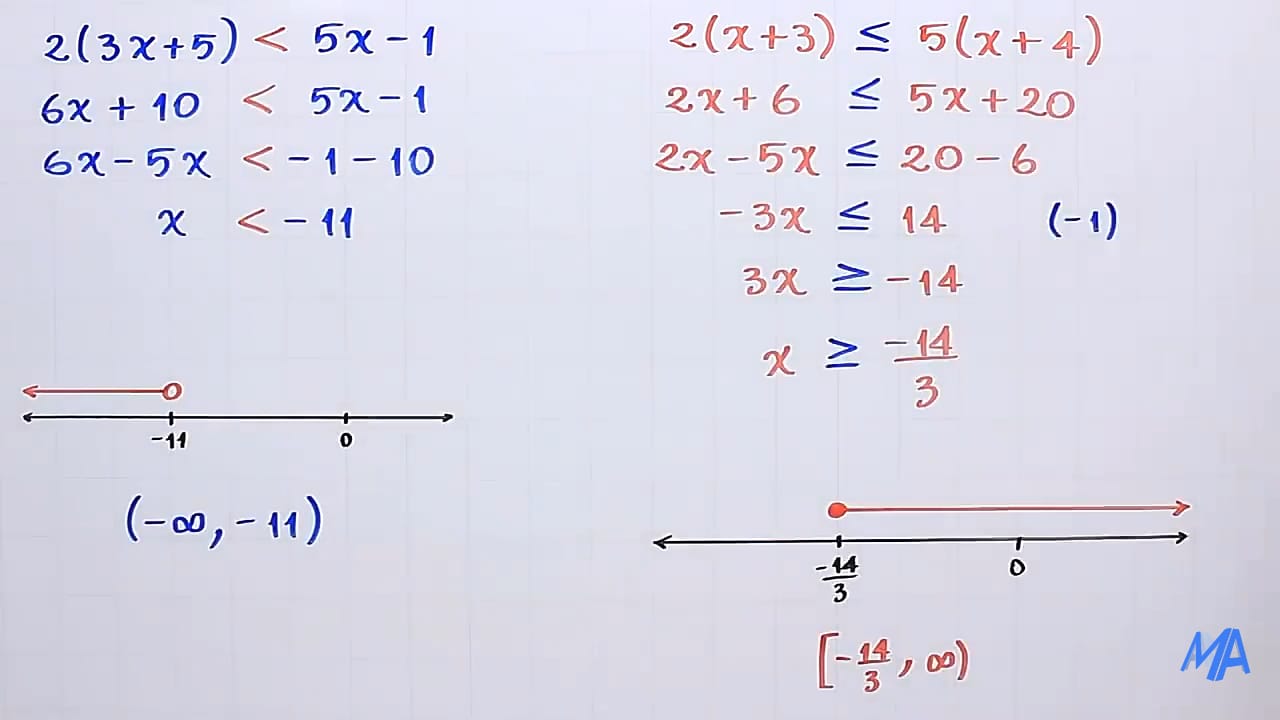




Comentarios
Publicar un comentario