Propósito de la sesión:

Usamos diversas representaciones para comprender las propiedades de las operaciones con números enteros, establecemos relaciones entre datos y las transformamos en expresiones numéricas con números enteros.

Saberes previos:

Analiza la siguiente imagen y responde:

¿A qué altura se encuentra el helicóptero del barco?,

¿a qué profundidad se encuentra submarino hundido con respecto al barco?,

¿Para qué nos sirven los números enteros?

Recordemos:

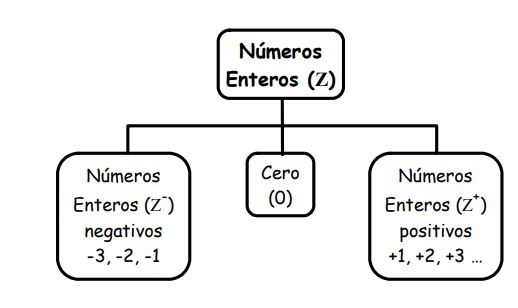
LOS NÚMEROS ENTEROS (Z)

Es el conjunto formado por los números enteros positivos, el cero y los números enteros negativos.

El cero no se considera ni positivo, ni negativo, es neutro.

Los números enteros nacen al no poder dar respuesta a situaciones cómo: representar temperaturas bajo cero, dinero que se debe, profundidades, etc.

Los números enteros negativos expresan cantidades que son menores que CERO y los enteros positivos cantidades mayores que CERO.

El conjunto de los números enteros se simboliza con la letra Z.

Observación:

Ordenación de números enteros:

Los números enteros se representan ordenados en la recta numérica:

En la recta puedes ver que cualquier número es mayor que otro que esté a su izquierda y menor que otro que este a su derecha. Por tanto:

Cualquier número positivo es mayor que el cero, y el cero es mayor que cualquier número negativo. Ejemplo: +5 >0, 0 >-5
Cualquier número positivo es mayor que cualquier número negativo. Ejemplo: +5 > -2, +5 > -5, +5 > -13.
Los números negativos se ordenan al revés que los positivos. Es decir, cuanto mayor sea la cifra, sin considerar el signo, menor es el número. Ejemplo: -1>-2, -2>-7, -12>-120.

Opuesto de un número entero:

Es el número que tiene el mismo valor numérico, pero con diferente signo. Así:

a) El opuesto de +8 es -8

b) El opuesto de -15 es +15

Valor absoluto de un número entero:

Se denomina valor absoluto de un número entero a la distancia que hay en la recta numérica, entre ese número y el cero.

Se denota con dos barras verticales a los lados del número, para referirnos al valor absoluto.

Así:

a) l-5l se lee, "valor absoluto de negativo cinco"

b) l+8l se lee, "valor absoluto de positivo ocho"

Ejemplos de valor absoluto:

a) l-6l = 6

b) l+6l = 6

c) l-10l = 10

d) l -5 +8 l = l +3l = 3

e) l -18 + 7 l = l -11 l = 11

Adición de números enteros:

A. Primer caso:

Para sumar dos números enteros con signos IGUALES, se suman sus valores absolutos y se coloca el mismo signo.

Ejemplos:

a) (+3)+(+4)=+3 + 4 = + 7

Porque l+3l + l+4l = 7 y ambos números tienen el signo (+).

b) (-2)+(-8)= -2 - 8 = -10

Porque l-2l + l-8l = 2 + 8 = 10 y ambos números tienen el signo (-).

B. Segundo caso:

Para sumar dos números enteros con signos DIFERENTES, se restan sus valores absolutos y se coloca el signo del mayor valor absoluto.

Ejemplos:

a) (+8) + (-5)=+ 8 - 5 = +3,

Porque se restan sus valores absolutos:

l8l - l-5l = 8 - 5 = 3 y se coloca el signo del mayor V.A. que es (+).

b) (-12) + (+8) =- 12 + 8 = -4

Porque se restan sus valores absolutos:

l-12l - l8l = 12 - 8 = 4 y se coloca el signo del mayor V.A. que es (-).

C. Tercer caso:

Para sumar varios números enteros con diferentes signos, tenemos dos métodos:

Primer Método:

Se suman separadamente los números enteros positivos y negativos, luego se suman los enteros positivos y enteros negativos obtenidos.

Ejemplos:

a) (-2)+(+4)+(-6)+ (-1)+(+10)+(+5)+(- 3)

[4 + 10+5]+ [(-2)+(-6)+ (-1)+(- 3)]

19 + (-12) = +7

b) (+4)+(-1)+(-5)+(-11)+(+22)+(-18)

[+4 +22]+[(-11)+(-1)+ (-5)+ (-18)]

+ 26 +(- 35) = -9

c) (-4)+(+6)+(-8)+(+15)+(-10)

[(-4)+(-8)+(-10)] +[+6 +15]

-22 + 21 = -1

Segundo Método:

Se suman los términos de la adición, de dos en dos y de izquierda a derecha.

Ejemplos:

a) (-2)+(+4)+(-6)+ (-1)+(+10)+(+5)+(- 3)

[(-2)+(+4)]+[(-6)+ (-1)]+[(+10)+(+5)]+(- 3)

[(+2)+(-7)]+ [(+15)+(- 3)]

(-5) + (+12) = +7

b) (+4)+(-1)+(-5)+(-11)+(+22)+(-18)

[(+4)+(-1)]+[(-5)+(-11)]+[(+22)+(-18)]

[(+3)+(-16)]+(+4)

(-13)+(+4)= -9

c) (-4)+(+6)+(-8)+(+15)+(-10)

[(-4)+(+6)]+[(-8)+(+15)]+(-10)

(+2)+(+7)+(-10)] = -1

Sustracción de números enteros:

Para restar dos números enteros, se le suma al minuendo el opuesto del sustraendo (Se aplican las reglas de adición).

Ejemplos:

a) (-6)-(+8)=(-6)+(-8)=-14

b) (-10)-(+22)= (-10)+(-22)=-32

c) (16) - (-6)= 16+6=22

d) 9 - (-1)= 9+(1)=10

Desarrollo:

Situaciones significativas:

"Problemas de la vida diaria"

Observaciones:

Como en los negocios se dan situaciones de ganancias y pérdidas; podremos interpretarlo asignando números positivos a las ganancias y números negativos a las pérdidas.

A las alturas sobre el nivel del mar, le asignaremos números positivos y a las profundidades debajo del nivel del mar, le pondremos negativos.

A las temperaturas mayores a 0 °C, asignaremos números positivos y las temperaturas por debajo de 0 °C, las representaremos con números negativos.

Más ejemplos: